Lens Formula - Equation

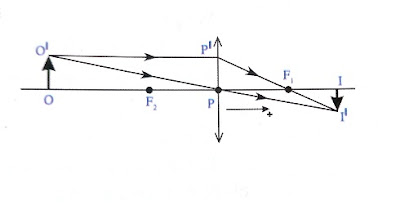
1. Consider an object OO’ placed along the principal axis.

2. Consider two rays emerging from the object. The first ray moves parallel to the principal axis and falls on the lens and thereby gets refracted and passes through the focal point F1.

3. The second ray passes through the optic center P and meet the first ray at the point I’.

4. This point I’ is the image of the point O’. Since the object is along the principle axis  The image of the point O will be also on the principal axis and let it be I.

5. II’ is the inverted image of the object OO’.

6. From the figure, we can say that PO is the object distance, PI is the image distance, PF1 is the focal length.

7. Consider two triangles from the figure.  ΔPP’F1 and ΔF1II’ are similar triangles.

PP’/II’ = PF1/F1I ------------ (1)

But F1I = PI – PF1

PP’/II’ = PF1/(PI – PF1)-------(2)

Consider another two triangles OO’P and PII’

OO’/II’ = PO/PI--------- (3)

But here OO’ = PP’

PP’/II’ = PO/PI

From equation (2) and (3)

PO/PI = PF1/(PI – PF1)

PI/PO = (PI – PF1)/PF1

PI/PO = PI/PF1 – 1

Divide both sides by PI

1/PO = 1/PF1 – 1/PI

1/PO + 1/PI = 1/PF1 ------------(4)

Sign convention

Here PO= -u (opposite to incident ray)

PI = v (same direction to incident ray)

PF = f

By substituting these values we get,

   1/v – 1/u = 1/f ---- this equation is called Lens Formula.