Lens maker’s formula - Equation

1. Place a thin lens (which is made of one convex surface and one concave surface) between two refractive indices.

2. Let n_a be the refractive index of one medium and and n_b be the refractive index of second medium.

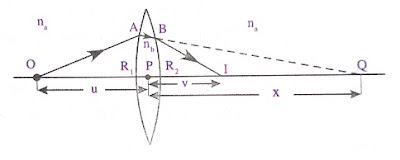
3. Consider an object O placed on the principal axis of the thin lens.

4. Now consider a ray from object O incident on the convex surface  of the lens at point A which has a radius of curvature R₁.

5. If there is no concave surface, it forms an image at Q then we take,

Object distance PO = -u, image distance PQ = v = x, radius of curvature R = R₁

6. For convex surface, n₁ = n_a, n₂ = n_b

7. According to image formation on curved surface formula,

n₂/v – n₁/u = (n₂ – n₁)/R

By substituting the values we get,

n_b/x + n_a/u = (n_b - n_a)/R₁ -----------------(1)

8. After getting refracted at point A again the ray get refracted due to concave surface at point B and reaches on the principal axis at point I.

Note: The image Q of object O due to the convex surface is taken as the object for the concave surface.

Here,

Object distance PQ = u = x, Image distance = PI = v, radius of curvature = -R₂

For concave surface n₁ = n_b, n₂ = n_a

by substituting the values we get,

n_a/v – n_b/x = (n_a - n_b)/(-R₂) ---------------- (2)

Add eq (1) and (2) we get,

n_a/v + n_b/u = (n_b - n_a)(1/R₁ + 1/R₂)

devide both sides by n_a,

1/v + 1/u = (n_ba - 1)(1/R₁ + 1/R₂)

here n_ba = n_b/n_a, is called the refractive index of lens with respect to the surrounding medium.

By using sign convention we get,

1/v – 1/u = (n_ba - 1)(1/R₁ – 1/R₂)

but we k now,

1/f = 1/v – 1/u

therefore we get,

1/f = (n_ba - 1)(1/R₁ – 1/R₂)

if the surrounding medium is air then n_ba = n

1/f = (n - 1)(1/R₁ – 1/R₂) is the equation of Lens Maker’s Formula.

Note:

1. The convex lens act as converging lens (if refractive index of medium is less than refractive index of lens)

2. The convex lens acts as diverging lens (if refractive index of medium is greater than refractive index of lens)

Lens Formula - Equation

1. Consider an object OO’ placed along the principal axis.

2. Consider two rays emerging from the object. The first ray moves parallel to the principal axis and falls on the lens and thereby gets refracted and passes through the focal point F1.

3. The second ray passes through the optic center P and meet the first ray at the point I’.

4. This point I’ is the image of the point O’. Since the object is along the principle axis  The image of the point O will be also on the principal axis and let it be I.

5. II’ is the inverted image of the object OO’.

6. From the figure, we can say that PO is the object distance, PI is the image distance, PF1 is the focal length.

7. Consider two triangles from the figure.  ΔPP’F1 and ΔF1II’ are similar triangles.

PP’/II’ = PF1/F1I ------------ (1)

But F1I = PI – PF1

PP’/II’ = PF1/(PI – PF1)-------(2)

Consider another two triangles OO’P and PII’

OO’/II’ = PO/PI--------- (3)

But here OO’ = PP’

PP’/II’ = PO/PI

From equation (2) and (3)

PO/PI = PF1/(PI – PF1)

PI/PO = (PI – PF1)/PF1

PI/PO = PI/PF1 – 1

Divide both sides by PI

1/PO = 1/PF1 – 1/PI

1/PO + 1/PI = 1/PF1 ------------(4)

Sign convention

Here PO= -u (opposite to incident ray)

PI = v (same direction to incident ray)

PF = f

By substituting these values we get,

   1/v – 1/u = 1/f ---- this equation is called Lens Formula.

Question: A bird is flying down vertically towards the surface of water in a pond with constant speed. There is a fish inside the water. If that fish is exactly vertically below the bird, then the bird will appear to the fish to be?

A bird is flying down vertically towards the surface of water in a pond with constant speed. There is a fish inside the water. If that fish is exactly vertically below the bird, then the bird will appear  to the fish to be?

1. farther away than its actual distance.

2. closer than its actual distance.

3. moving faster than its actual speed.

4. moving slower than its actual speed.

Sol. According to the image formula for refraction at plane surface. Here river water surface acts as a plane surface.

We have n2/v = n1/u

Let x be the height of the bird at O above the water surface and y be the height of the image at I.

Here n1 = 1 (refractive index of Air)

          n2 = n (refractive index of water)

According to sign convention,

Height measured vertically above from the point of axis is taken as positive and below is taken as negative.

Therefore u = x (object distance vertically above)

                    V = y(image distance vertically above)

n/(y) = 1/(x)

y = nx from above expression which we got, we can say that n is greater than 1 and therefore y is greater than x.

So from this we can say that bird appears to fish to be farther away from the actual distance and it appears to fish that the bird covers more distance i.e y distance than the actual x distance. It appears that the speed of the bird is greater than the actual speed.

Image Formation Formula For Curved Surfaces

1. Let us consider a curved surface separating two media of refractive indices n1 and n2.

2. Let n1 be the rarer medium and n2 be the denser medium.

3. An object is placed on the principle axis at a point O in the rarer medium.

4. Consider two rays coming from the object O.

5. The first ray travels along the principal axis meet the pole and the refracted ray passes through the pole undeviating .

6. The second  ray making an angle α with the principal axis strikes the curved surface at the interface at A.

7. Let the angle of incidence be θ1.  The refracted ray passes through the denser medium and meets the principal axis at point I. Let the angle of refraction be θ2.

8. The two refracted rays meet at point I and there the image is formed.

9. Let the angle made by second refracted ray with principal axis be γ.

10. Let the angle between the normal and the principal axis be β.

11. Let the object distance (u) be PO and the Image distance(v) be PI. Let PC be the radius of curvature (R).

                  From  Δ ACO, θ1= α + β

                 From  ΔACI,  β = θ2 + γ

                        β – γ = θ2

   We know that according to Snell’s law,

        n1 sin θ1 = n2 sin θ2

  Substituting the values of θ1  and θ2

       n1 sin (α+β) = n2 sin(β-γ)

 12.  The angles α,β and γ is considered as very small if the rays are very close to the principal axis . Since the rays are parallel to the principal axis, they are called paraxial rays and this approximation is called paraxial approximation.

                  Therefore sin(α+β) = α+β and sin(β-γ) = β-γ

n1 (α+β) =  n2 (β-γ)

n1 α + n1 β = n2 β - n2 γ

And Tanα = AN/NO

Tanβ = AN/NC

Tanγ =AN/NI

Since all angles are very small,

    α = AN/NO

β = AN/NC

γ = AN/NI

substituting the angle values, we get

n1 AN/NO + n1 AN/NC = n2 AN/NC – n2 AN/NI

here N becomes P(POLE)

n1/PO + n1/PC = n2/PC – n2/PI

n1/PO + n2/PI = (n2 – n1)/PC

Sign Convention:

All the distance are measured from the pole

Distance measured in the direction of the incident ray are taken as positive and in opposite direction is taken as negative.

The height measured above the axis is taken as positive and below the axis is taken as negative.

Here PO= object distance = -u

PI= image distance = v

PC= radius of curvature= R

 By substituting the values, we get  

                      n2/v – n1/u = (n2 – n1)/R , for curved surfaces. 

Note: For plane surface, radius of curvature (R) approaches infinity then 1/R becomes 0. Therefore,

For plane surfaces,

n2/v – n1/u = 0

                                   n2/v  =  n1/u